HashMap
继承关系
Map以键值对(KV)储存数据,是java中的众多集合类中的一个接口,定义在包java.util中:
1 | public interface Map<K,V> |
AbstractMap是一个继承了接口Map的抽象类:
1 | public abstract class AbstractMap<K,V> implements Map<K,V> |
AbstractMap作为一个抽象类,其最常用的实现类就是HashMap,同时HashMap继承了接口Cloneable和Serializable:
1 | public class HashMap<K,V> extends AbstractMap<K,V> implements Map<K,V>, Cloneable, Serializable |
基本使用
put存键值对
1 | public V put(K key, V value) |
get取键值对
1 | public V get(Object key) |
isEmpty判断是否为空
1 | public boolean isEmpty() |
时间复杂度
HashMap被使用得最多是因为为哈希表高效的性能,插入删除查找的时间复杂度都为$O(1)$,对比其他数据结构:
| 数据结构 | 插入 | 删除 | 查找 |
|---|---|---|---|
| HashMap | $O(1)$ | $O(1)$ | $O(1)$ |
| ArrayList | $O(N/2)$ | $O(N/2)$ | $O(1)$ |
| LinkedList | $O(N/4)$ | $O(N/4)$ | $O(N/4)$ |
| 二叉树 | $(logN)$ | $(logN)$ | $(logN)$ |
基本结构
HashMap由数组和链表构成。这个数组在源码中被称为table,table中存放的每一个元素都是一个被称作bin的容器,bin是一个由类Node构成的一个链表,其中类Node继承自Map.Entry。所以实质上,HashMap就是一个储存了Node的数组。数组中每个Node为所在bin的链表头,指向该bin中的下一个Node,这里的每一个Node就是我们键值对实际储存的地方,包含了key和value。(这是最开始的简单情况,后文将提到,当每个bin中的Node数量超过一定值时,为了提高效率这个链表将转换成二叉树)
每次插入新包含键值对的Node,它要么落在数组空的位置,直接被放入,要么落在已经数组中已经存在Node的位置,这种情况的话将遍历这个占了位置的Node所连接的链表,将新的Node接这个链接的尾部。
那如何知道这个新的Node插入在数组的什么位置呢,用什么样方式确认新的Node的数组下标呢?答案是对Node的key求哈希,将这个哈希值映射到数组的长度中。用这样的方法,每一个键值对根据它的键key的哈希值必然有一个唯一的确定的下标。
我们每次做插入操作时,对要插入的key值求哈希,做一些处理使得这个哈希值映射到数组的一个下标值。现在已经有了确定的下标值了,如果下标志的位置没有Node,那就直接放入,如果有Node存在,插入到这个Node所在链表的尾部。查找操作也是一样的,求哈希,映射得到下标,遍历下标所在的位置的链表找到key值相等的Node,返回其value。
哈希碰撞
假设我们的数据运气很好,每次插入新的Node时,它都落在数组table空的位置,新的Node都是数组中的新元素,每个Node都是链表头并且没有下一个节点。这样插入的时间只有$O(1)$;这种情况每次查找时时间当然也只需要$O(1)$。这样的话HashMap效率非常可观。
但事实情况超出了以上美好假设的范围,由于哈希值非常大,在java中调用本地的hashcode()得到的哈希值是一个int值,32位整型。由于哈希值是一个长度固定的值,它是有限的,而我们的key其可能值可以说是无限的,对无限可能值的key做一样的哈希算法得到的哈希值,会有不同的key得到相同的哈希值的情况,这种情况叫做哈希碰撞。加上我们HashMap的table数组一开始初始化容量只有16,当容量不够时将会扩容,即便扩容,大部分实际情况下table的大小也远远达不到32位这个数量级。当32位的哈希值映射到table小小的容量的范围时,会发生不同的哈希值映射到table相同的下标的情况,更加加剧了不同的key对应table同一个下标的情况发生,于是出现了上文说的需要将新的Node插入到链表尾部的操作。
哈希碰撞发生比较频繁时,即不同key值映射到数组同一个下标的情况非常多时,会导致了数组table中不断插入的Entry分布不均匀,数组中一些位置是空的,一些位置的bin链表长度非常长。这样的话每次插入和查找的时间就完全做不到$O(1)$了,我们只有尽可能让这种情况发生次数减少,让Entry在table中均匀分布,让HashMap的操作时间接近$O(1)$。
哈希散列为下标
为了将32位的哈希值映射到数组容量的大小中,并让这些哈希值的映射尽可能地在table的0到length-1间分布均匀,我们想到的最简单的方法就是将得到的key哈希值对table的长度length求模,这样32位的哈希值就映射在了0到length-1的范围中。
这样解决了大范围映射到小范围的问题,但依然没有解决如何让哈希映射到下标更加均匀。阅读源码,我们发现源码中做了将哈希值的高16位和低16位进行异或运算的操作,之后再去求模。
我们可以这样理解,当table容量不够大,远远比哈希值的32位小的时候,我们对哈希值取table长度的模,哈希值的高位往往对这个结果没有影响。
举例以下两个哈希值取16的模:
1111 1111 1111 1111 1111 1111 1111 0101
0000 0000 0000 0000 0000 0000 0000 0101
虽然这两个值只有低4位相同,高28位完全不同,可它们取16的模结果却完全一样,因为影响这个结果只有低4位,因为16换成二进制的最高位数为只有5位。当我们将高16位与低16位做异或操作时,
上面第一个数的低4位成了:1111 ^ 0101 为 0101
上面第而个数的低4位成了:0000 ^ 0101 为 1010
这时候他们取模16的结果将不一样了。这种做法本质上是将低位变成高位的信息特征与低位信息特征的融合。让低位的数据同时有了高位和原本低位的信息特征,为之后映射到数组table下标增加了均匀性。
做完异或操作后将得到的新的哈希值对数组长度取模即可得到数组table的下标。
为了优化取模的效率,在HashMap源码里面table的长度规定为2的整数幂,将取模操作转换成了位操作,因为当length为2的整数幂时,hash % length可以变换成hash & ( length -1 )。位操作比取模操作更快。
我们重头看一遍下标是如何获得,并且让大量的key更均匀的映射到table下标范围的:
key调用本地方法hashCode()得到自身的int类型哈希值。将这个32位的哈希值高16位和低16位做异或操作得到新哈希值
hash。将新哈希值
hash取table长度length的模,并优化成位运算hash & ( length -1 )。
最后求得的模,即位操作的结果就是下标。
扩容
当HashMap第一次存入键值对时,会执行一次方法resize(),table的容量,扩容临界值才被初始化。
1 | static final int DEFAULT_INITIAL_CAPACITY = 1 << 4; |
1 | static final float DEFAULT_LOAD_FACTOR = 0.75f; |
1 | newCap = DEFAULT_INITIAL_CAPACITY; |
1 | threshold = newThr; |
可见初始容量为16(1<<4),threshold为触发扩容操作的临界值,初始值为12(0.75*16),即当前容量的0.75。
每次存入键值对时,若包含键值对的Node添加在table的空位置中而不是某位置所在的Node链表尾部,table数组的长度size加1后,进行检查,若size大于临界值threshold,执行方法resize()。也就是说**HashMap的扩容条件是数组table长度szie超过了容量的0.75**。
1 | if (++size > threshold) |
在resize()中,table的容量进行了翻倍,同样临界值threshold也翻倍,此时仍然是容量的0.75。
接下来是非常重要的部分,我们新设置了一个容量为翻倍后的数组,遍历旧数组中的每一个Node,将其重新映射(散列)到新数组中。
首先遍历数组,当数组中的元素为空时跳过
当数组中的元素为单个Node时,重新用位操作来快速根据新容量的大小求模的到新数组的下标,直接将Node放入。
当数组中的元素为红黑树时 (后面补充)
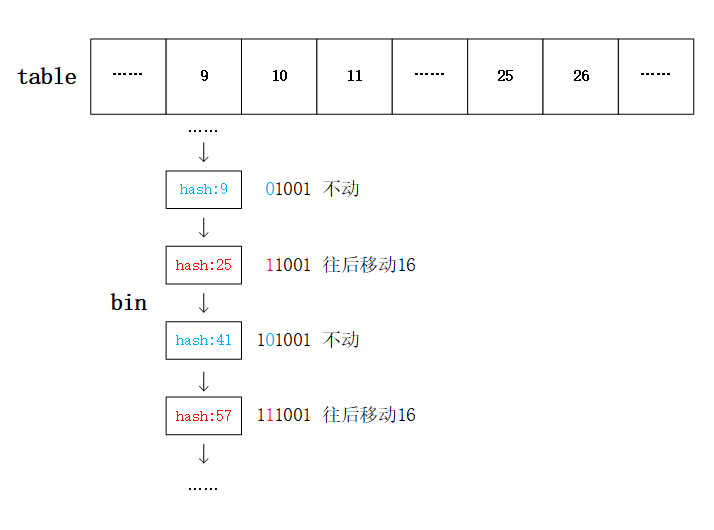
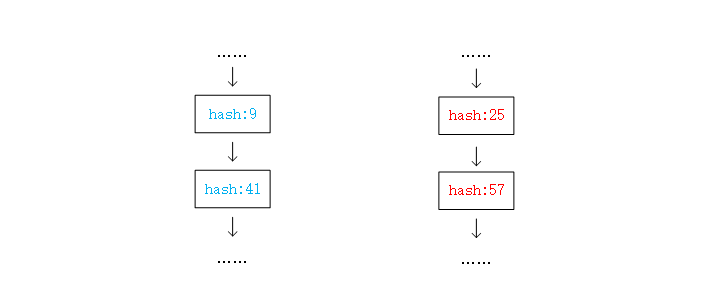
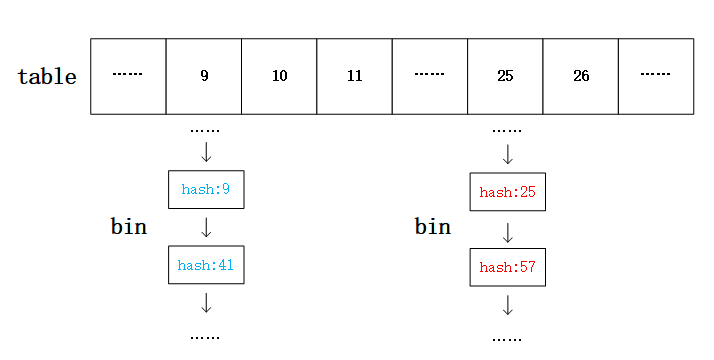
当数组中的元素为Node的链表时,遍历链表求每一个Node在新数组中的下标。由于我们的扩容是翻倍扩容,新数组的容量为旧数组的2倍,所以新数组中每一个Node的位置(下标)必然是它在旧数组中的原位置或者原位置加上增加容量的偏移,换句话说,旧数组中的Node搬新数组,要么下标不变,要么往后移动一个增加的容量大小的距离。例如当旧数组的原容量为16时有哈希值分别为9,25,41,57的四个Node,把这四个Node搬去容量翻倍为32的新数组时,哈希值为9的Node原地不动,因为它求模32后依然下标为9,和旧容量16时求模结果一样;哈希值为25的在原数组中求模为9,跟哈希值为9的Node同属一个bin的链表中,但在新数组中求模为25,于是在新数组中搬去了下标为25(9+16)的位置,与它本来原位置9偏移了一个扩容的大小16(原数组的容量);接着看哈希值为41的Node,它在旧数组和新数组中的求模都为9,所以是呆在原位置不需要移动;57与25同理。我们发现,像哈希值9,25,41,57在16容量搬去32容量的例子下,我们只需要判断它们被32求模了之后再求模16的结果是不是为0,也就是判断它们被32求模了之后的值是否“溢出”16?或者说比16大还是小?如果“溢出”16,则需要搬位置,往后位移16,否则原地不动。所以这样看来,我们不必对链表中每一个Node的哈希值去求模取得新下标,我们只需要判断它是否是呆在原地还是往后位移一个增加容量的距离即可。源码中判断“是否溢出16”用了效率比较高的做法,直接去判断哈希值的二进制在第5低位上是不是1即可,第5位即为16的最高位(二进制10000),如果这个位上为1,证明被32求模的结果大于等于16,如果为0则小于16。最终,我们只需要在操作上将哈希值和旧容量(最高位为1其他位都为0,如16的二进制10000)的值做与运算,判断结果是否为0。下一步来说,我们当前是在遍历一个链表,我们把需要位移的Node拿出来组成新链表,放去位移的位置,剩下原地不动的Node重新接成一个链表,留在原地。这样处理的明显好处是链表中Node之间的前后关系没有发生变化。