AVL树的旋转
特定例子
现在我们开始解决AVL树中提到最小不平衡子树,使AVL树重新恢复平衡状态。
下图先举例一个最简单的平衡的AVL树在经过插入操作后变得不平衡的例子
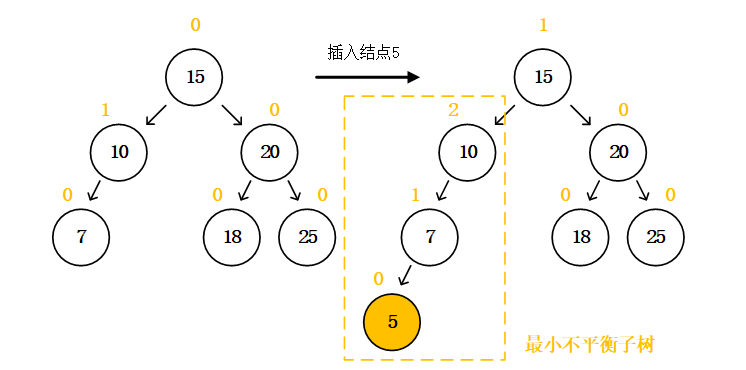
如图所示插入结点5后,父结点7的平衡因子变为1,再往上的父节点10变为2,这个结点10就是我们要找的最小不平衡子树的根结点。我们把最小不平衡子树拿出来单独讨论。
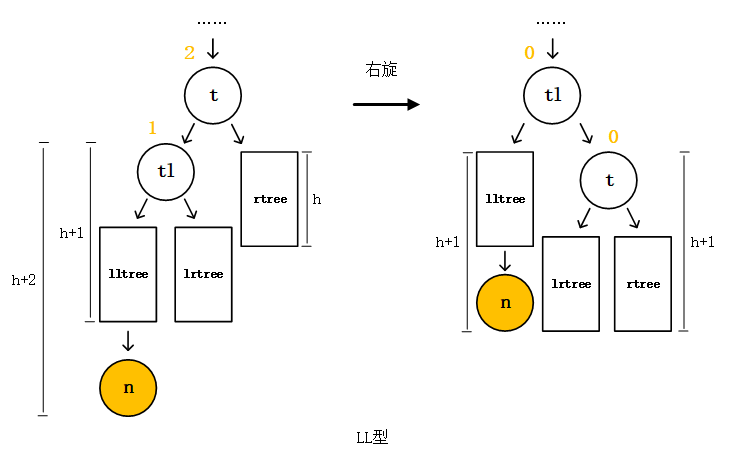
这是最简单的情况,最小不平衡子树的根结点为结点10,新插入结点5是根结点10的左子结点的左子结点,这种情况我们成为LL型(左左型)。在LL型中,根结点10比它的左子结点大,它的左子结点也比新插入的结点大,我们可以把这三个结点的位置转一转,把结点10转到结点7的右下方,也就是从结点7的父节点变成了结点7的右子结点,而结点7自己成了根结点
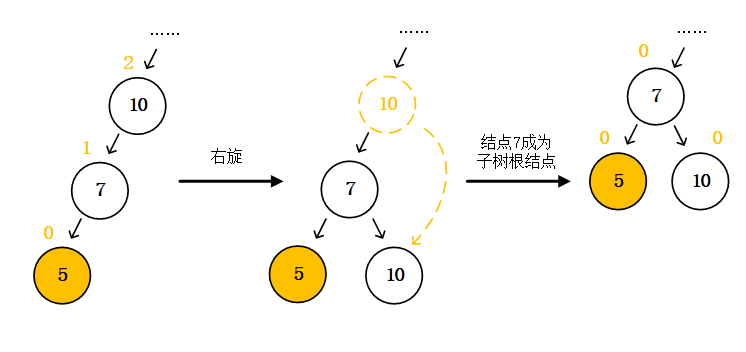
现在以结点7为根结点的子树平衡了,整个树也就重新达到AVL的平衡条件了。我们旋转的对象是根结点10,根据它的旋转方向我们称这种旋转为右旋。所以LL型我们只需要一次右旋就能重新回归平衡。因为结点10和结点7之间的大小关系,所以结点10既能做结点7的父结点,也能做结点7的右子结点,右旋操作就是将操作结点从父结点变为右子结点。
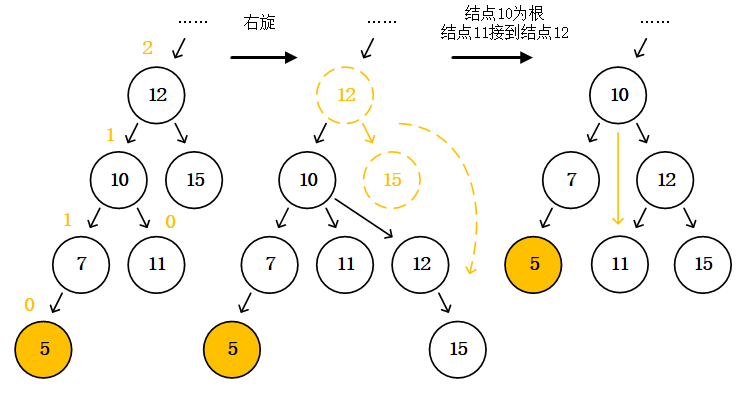
这个LL型过于简单,再举个LL型的最小子树例子,下面这个例子的子树高度比上面那个例子要高,但同样只需要一次右旋就能回到平衡状态。
完全对称的,我们也有RR型(右右型),所以对称地我们需要一次左旋来让RR型回归平衡,我现在把LL型的例子变成RR型,再看看示意图,完全是对称的操作。右旋操作就是将操作结点从父结点变为左子结点。

LL型
例子举完了,现在该分析一下所有可能存在的情况了。如下图,设想现在有一个子树的根结点t,子树处于平衡状态,它的左子树我们先记做ltree,右子树我们记做rtree。左子树和右子树中的结点数未知,但是它们的高度差因为平衡所以一定不大于1。现在我们插入一个新的结点n,假定我们插入新的结点之后,树将不再平衡,并且这个以结点t为根的子树是整个树的最小不平衡子树。那只有两种插入情况,一种是插入在左子树上,左子树比右子树高2,一种是插在右子树上,右子树比左子树高2,我们把比较矮的一边子树的高度记做h,则另一边比较高的子树的高度为h+2。当然h必须h≥0。可以想象到这两种情况是对称的,那他们解决平衡的操作也是对称的。
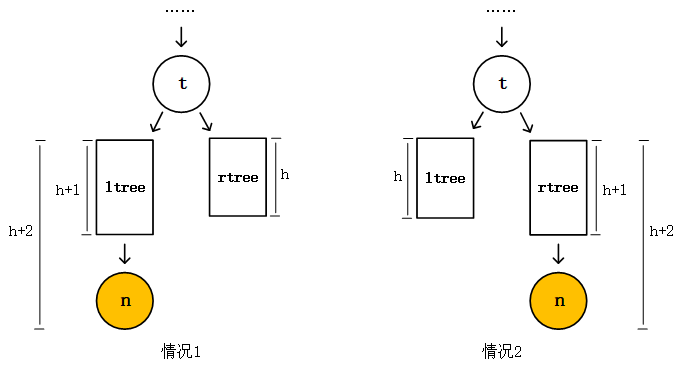
我们现在拿情况1出来分析,把ltree又分为它的根结点tl和tl的左子树lltree和右子树lrtree,同样有两种情况,结点n要么是接在lltree上要么是接在lrtree上,根据上面的讨论,高度如下图所示,同时我也标注好了平衡因子。
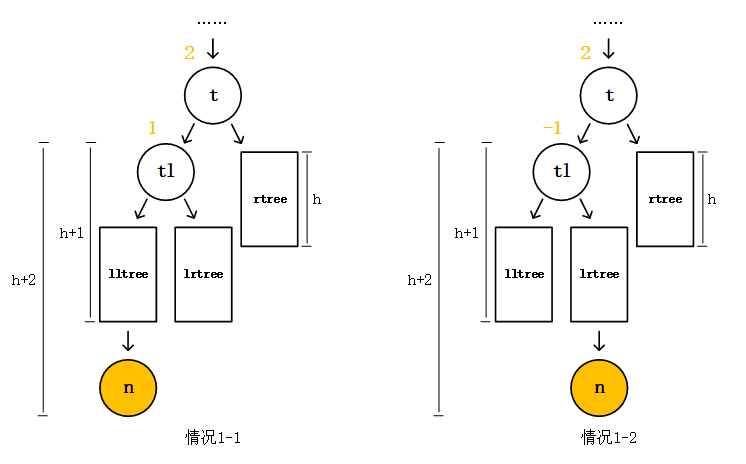
注意!以上的讨论都是建立在结点t构成的子树为最小不平衡子树下。因为这个子树为最小不平衡子树,所以必然的,情况1-1中lltree和lrtree还有rtree三个子树的高度都相等都是h,情况1-2中rltree和rrtree还有ltree三个子树的高度也相等也都是h。h要满足h≥0。反过来说lltree和lrtree还有rtree(或是rltree和rrtree还有ltree)它们的高度不可能不相等,如果不相等那结点t构成的子树就不是最小不平衡子树,记住我们所讨论的情况都是建立在结点t是最小不平衡子树的根结点上的。
对于情况1-1我们可以继续分类讨论出情况1-1-1和1-1-2……但这样套娃已经完全没有必要了,因为我们现在就能针对情况1-1做出普适性的回归平衡方法。
现在我们针对情况1-1来看,发现上文中右旋的两个例子就是情况1-1,情况1-1即是LL型。当lltree和lrtree还有rtree的高度为0时,就是上文右旋的第一个例子,而这三个子树高度为1时,就是上文右旋中第二个例子。可以继续推导的是,lltree和lrtree还有rtree的高度h只要满足h≥0,这种最小不平衡子树都是LL型,能都通过对根结点t一次右旋重新回归平衡,如下图。
LR型
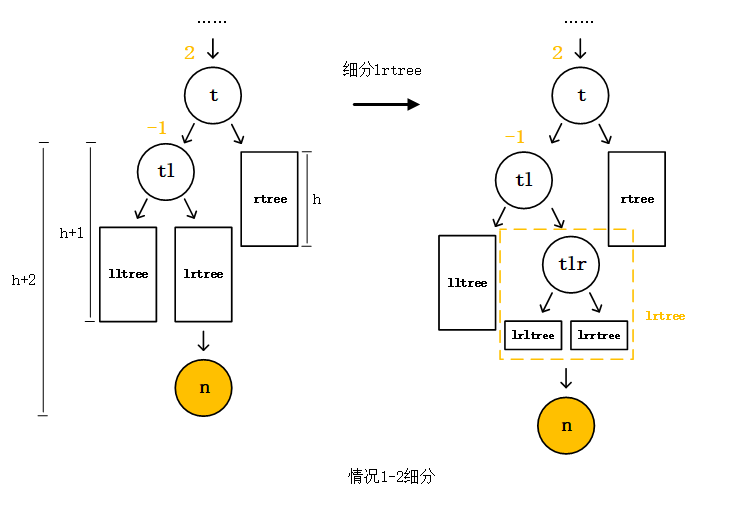
接下来讨论情况1-2,我们发现这不再是LL型了,我们无法通过一次右旋来解决问题,如下图:
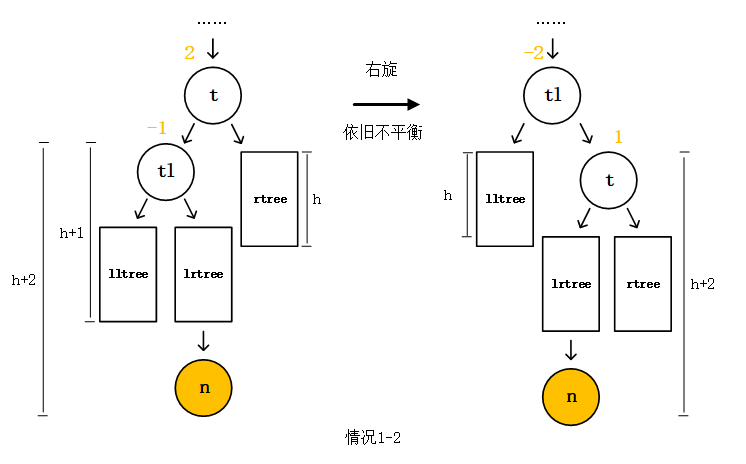
我们需要继续分析讨论情况1-2,分类讨论结点n插入的更准确的位置。我们把lrtree这个子树细分成结点tlr和其左右子树lrltree和lrrtree。我们对情况1-2分别得到以下两种情况1-2-a和1-2-b。1-2-a是结点n插在lrltree上,1-2-b是结点n插在lrrtree上。
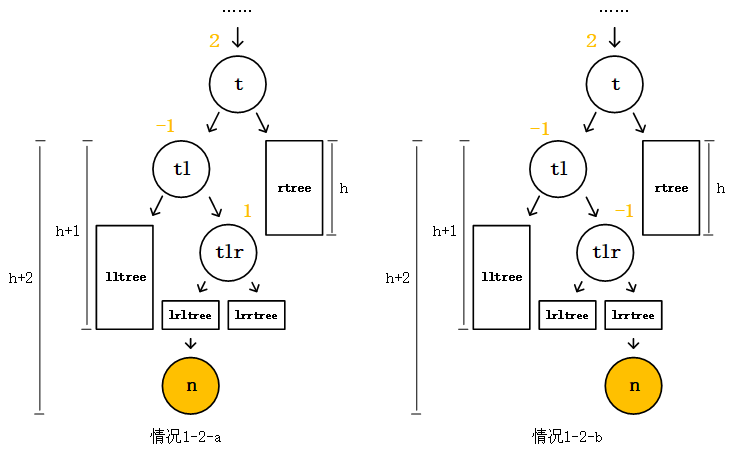
经过分析我们发现,虽然我们不能通过一次右旋来回归平衡,但是我们发现如果对情况1-2-a和1-2-b中的结点tl进行一次左旋,我们将把情况1-2-a和1-2-b转变了LL型,如下图
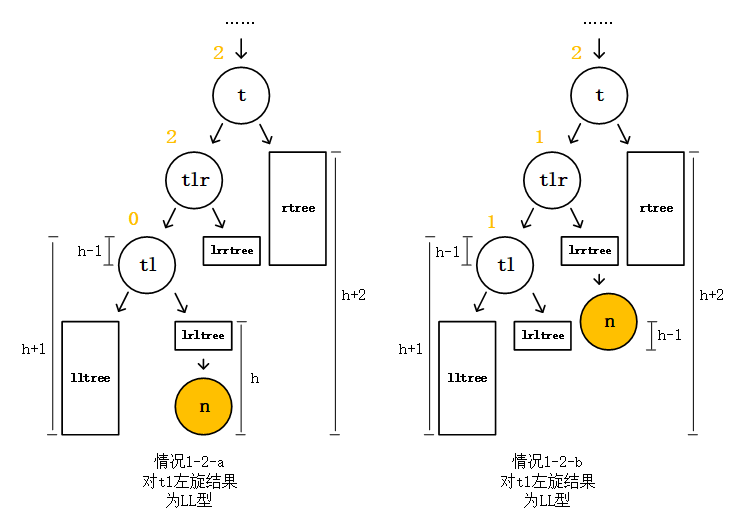
情况1-2-a和1-2-b进行了左旋之后,得到的LL型是有区别的,情况1-2-a左旋结果的结点tlr的平衡因子为2,最小不平衡子树变成了以结点tlr为根的最小不平衡子树,不是结点t。而情况1-2-b左旋结果的结点tlr的平衡因子为1,所以依然是以结点t为根结点的最小不平衡子树。对于情况1-2-a左旋结果,它的最小不平衡子树变了,虽然也是LL型,但是我们能对结点tlr做一次右旋让它回归平衡吗?答案是不能,这样又变回情况情况1-2-a了,左右旋本身就是互为反操作。那这样的话,我们依旧是把情况1-2-a左旋结果的最小不平衡子树当做没有变动,根结点依旧是结点t,所以对于情况1-2-a左旋结果和情况1-2-b左旋结果,这两个都是根为结点t的LL型,我们对结点t做一次右旋即可回归平衡。如下图。
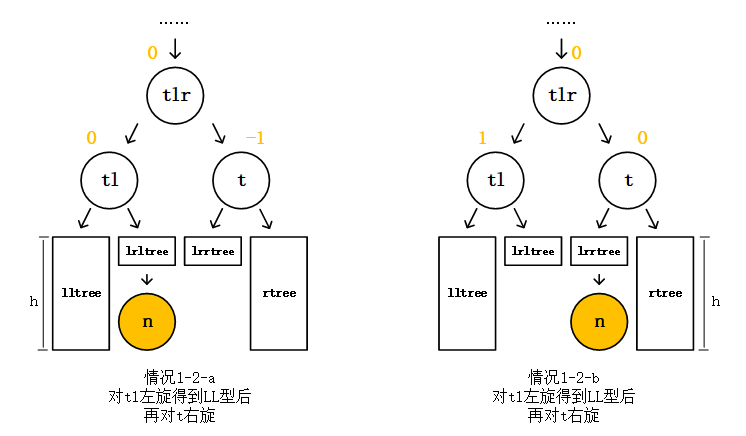
情况1-2细分的两种情况现在就已经解决了不平衡问题,方法都是先对结点tl做一次左旋,再对结点t做一次右旋,我们把情况1-2称作LR型。所以LR型的最小不平衡子树,我们先对根结点t的左子节点tl做左旋转换成LL型后,再对结点t做右旋,即可平衡。但LR型里面也是有区别的,虽然都是对结点一样的操作,可重新平衡之后结点t和结点tl的平衡因子是不一样的,在实现上要注意处理这个问题。
RR型和RL型
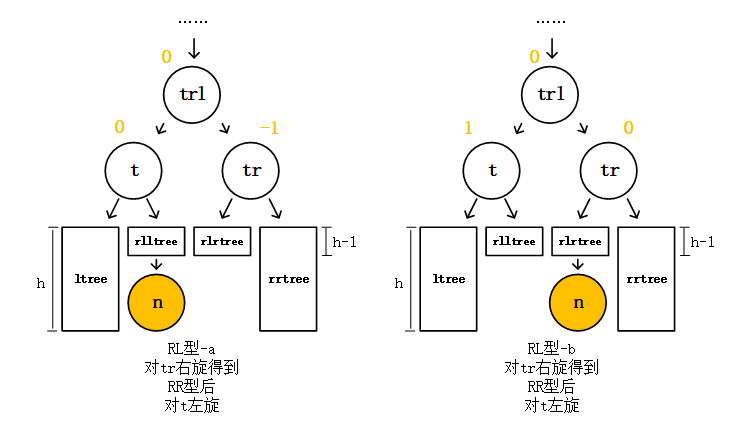
至此,其实我们已经解决掉AVL树的一半旋转方法了。LL型对根结点t做一次右旋,LR型对根结点t的左子节点tl做一次左旋再对结点t做一次右旋。对称地,我们可以得知,把LL型和LR型镜像翻转过来我们得到RR型,和RL型,重新平衡的操作也是对称的,对于RR型应当对根结点t做一次左旋,对于RL型应当对根结点t的右子结点tr做一次右旋,再对结点t做一次左旋。于是我们对于所有的不平衡情况都给出了平衡的旋转方法。下面示意图表示一下RR和RL的过程,就不从头分析一遍了。
RR型:
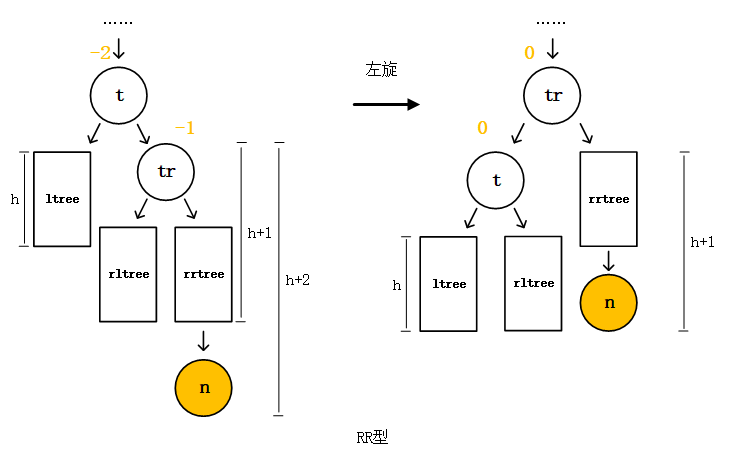
RL型
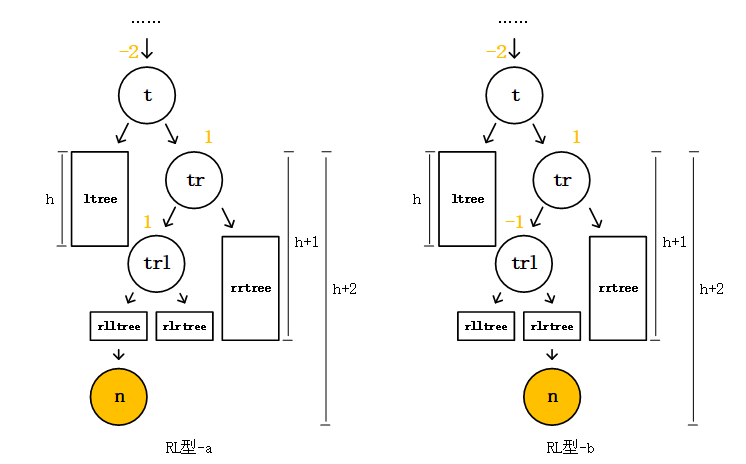
RL型对结点tr右旋转换成RR型:
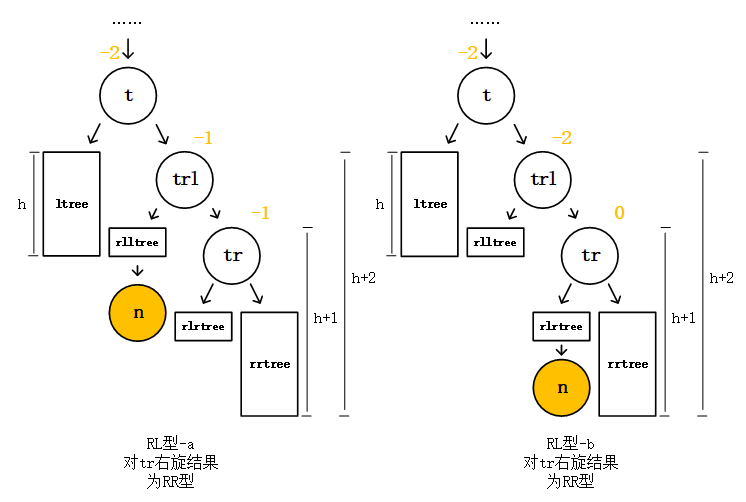
最后再对结点t左旋: