二叉树及二叉搜索树

发表于 更新于 分类于

二叉树

首先我们来看一个普通的链表，头节点指向下一个结点，下一个结点再指向下一个结点，直到尾部最后一个结点。这个单向链表的一个特征：除了最后一个结点外，每一个结点都指向下一个结点。

现在，那这个链表的中的结点，指向的结点不仅仅限定是一个，还允许是两个呢？

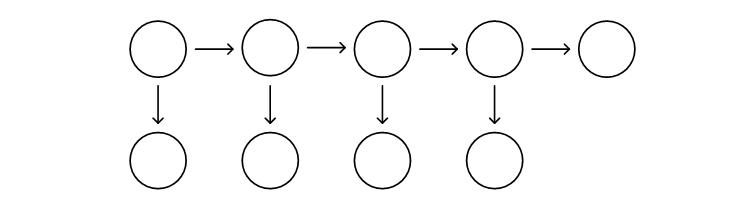
整理一下位置排版

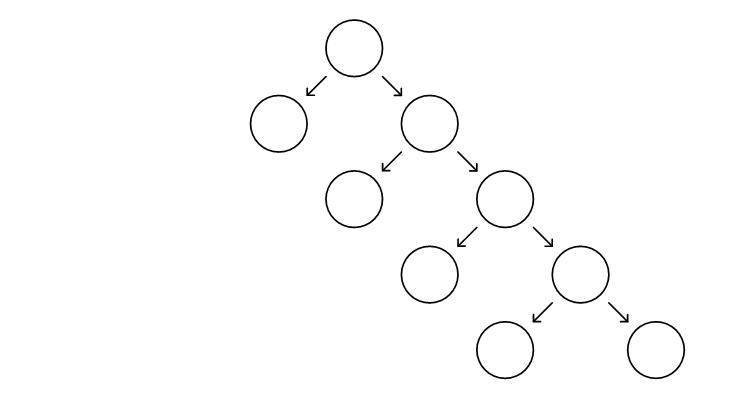
于是它变成了一个二叉树。二叉树在维基百科中的定义：二叉树（英语：Binary tree）是每个节点最多只有两个分支（即不存在分支度大于2的节点）的树结构。你也可以说上面的链表，它是一个极端条件下的二叉树，一个特殊的二叉树。数据的组织结构从来都不会凭空产生，而是根据需求不断变化不断适应。

每一个结点往下指的一个或两个结点，都称为它的子结点，而它被称作它们的父结点。相对左右的位置，它们分别被称为左子结点和右子结点，以左右子结点为根构成的子树被称为左子树和右子树。

二叉搜索树

现在我们给二叉树新加一个限定规则，如果存在一个结点存在它的左右子树的话，它的左子树上每一个结点的键都比它的键小，它的右子树上每一个结点的键都比它的键大。添加了这一个规则后，它便不仅仅是是一个普通的二叉树，而成了二叉搜索树，很明显，加入了左右子树结点键的大小限定规则后，这个二叉树变得有序了起来。

维基百科中二叉搜索树的性质定义：若任意节点的左子树不空，则左子树上所有节点的键均小于它的根节点的键；若任意节点的右子树不空，则右子树上所有节点的键均大于它的根节点的键；
任意节点的左、右子树也分别为二叉查找树。

插入

我们现在通过将数组8,4,3,9,7]作为键不断插入来形成一个二叉搜索树。首先第一个键为6，现在树还不存在，6作为树的根放入成为结点6；第二个插入8，在经过和根部结点6后，8比6大，结点8插在了结点6的右边，成为了结点6的右子结点；接着插入4,4比8小， 成为了8个左子结点；继续插入3，3比6小，应该插入到结点6的左子树中，再和结点6的左子结点4比较，3比4小，插入到4的左子树中成为4的左子结点。以这种方式一直将数据插入进去。

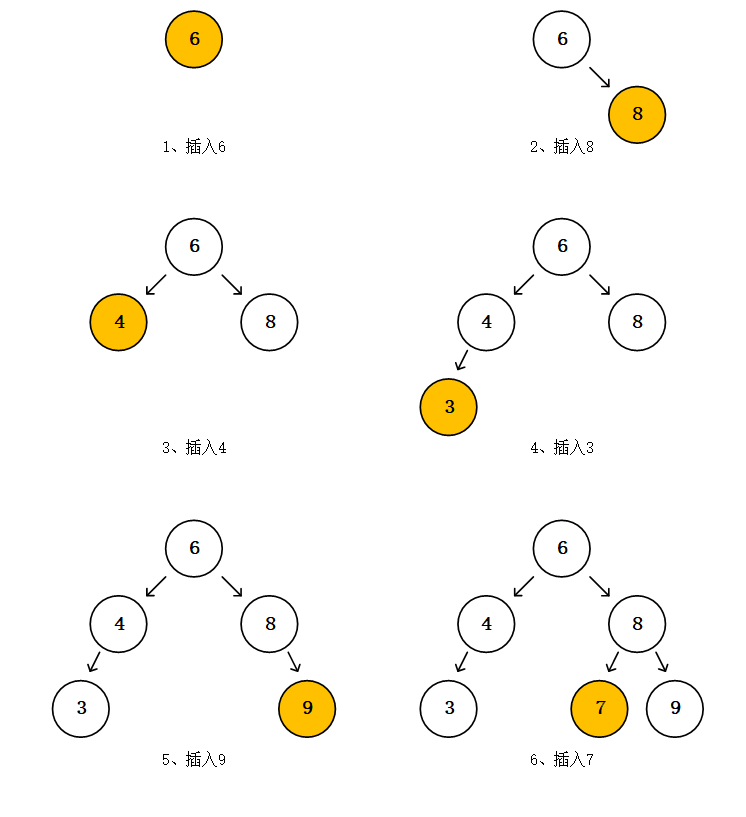
试着简单手动实现一下二叉搜索树的插入

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
public class BSTree {
	public TreeNode root;
    
	public boolean insert(TreeNode node) {
		if(root == null) {
			root = node;
			return true;
		}
		TreeNode parent = root;TreeNode nodeTmp = root;
		while(nodeTmp!= null) {
			parent = nodeTmp;
			if(node.key == parent.key) return false;
			nodeTmp = node.key < parent.key?parent.left:parent.right;
		}
		if(node.key < parent.key) {
			parent.left = node;
		}else{
			parent.right = node;
		}
		node.parent = parent;
		return true;
	}
}

注意，我们在讨论中默认二叉树的结点键不能有重复，如果有重复键需要额外讨论。

查找

我们接下来继续用上面插入好的二叉搜索树，试着从树里面查找出结点7。我们依然从根节点开始往下判断，判断当下结点和7的大小关系，若相等，即为要找的结点，若要查找的结点小于当下结点，意味着我们需要往当下结点的左子树中查询，把当下结点的左节点作为要判断的当下结点，反之我们需要往右子树中查询，把当下结点的右节点作为要判断的当下结点，循环步骤直到找到结点7，若当下结点一直往下直到为空，意味着树中不存在要找的结点。

试着手动实现一下二叉搜索树的查找

1
2
3
4
5
6
7
8
9
10
11
12
13
public TreeNode search(int key) {
    TreeNode nodeTmp = root;
    while(nodeTmp!=null) {
        if(key < nodeTmp.key) {
            nodeTmp = nodeTmp.left;
        }else if(key > nodeTmp.key) {
            nodeTmp = nodeTmp.right;
        }else {
            return nodeTmp;
        }
    }
    return null;
}

查找最大最小结点

我们想一下二叉搜索树的插入方式，当要插入一个结点时，从根部往下，遇到这个结点比当下判断结点小的，我们往左子树走，反之我们往右子树走，就像一个岔路口，我们不停的找方向，直到走到尽头，再把结点插入。很明显，若是插入一个比树当前所有结点都小的结点时，我们每经过一个岔路口都是往左，反之则往右。所以最小值在树的最左下角，从根结点一直往左子树走，走到没有左子树的结点就是最小结点，最大值亦然。

手动实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public TreeNode findMin() {
    TreeNode node = root;
    if(node == null) return null;
    while(node.left != null) {
        node = node.left;
    }
    return node;
}
public TreeNode findMax() {
    TreeNode node = root;
    if(node == null) return null;
    while(node.right != null) {
        node = node.right;
    }
    return node;
}

删除

删除的情况相对于插入和查找，需要一点思考。假设我们删掉二叉搜索树最底部的结点，即没有子结点的结点（我们一般称为叶子结点），我们直接将其父节点的左子结点或右子结点设为空，将其本身也设为空，就直接删去了，非常简单，因为没有其他影响。如删去结点7。

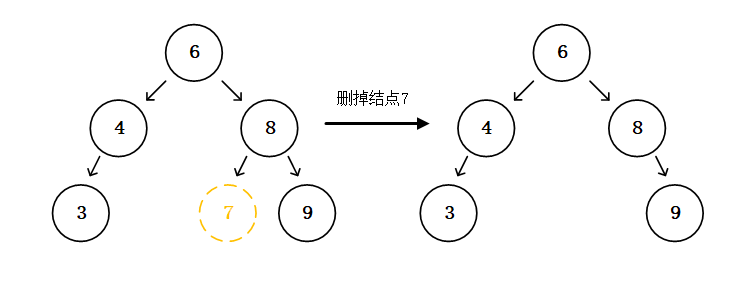
但如果删去结点6呢，或者结点8呢？结点6个结点8都有子结点/子树，这种情况下的删除操作需要考虑被删除结点的子树何去何从。其实，与其从处理被删除结点的子树的角度出发考虑，倒不如这样思考：用哪里的一个结点去替代这个被删除的结点？也就是说，拿去被删除的结点，用另一个结点换到这个位置上，保证二叉搜索树的限定条件依然成立。情况就变得非常简单了，拿掉一个结点之后，要找到一个比被删除结点的左子树都大又比被删除结点的右子树都小的结点，换去那个位置接上即可。而这个结点要满足条件，它只能是被删除结点的左子树中最大结点，或者是被删除结点右子树中最小结点。

举例删除结点6来说，我们先看看删去结点6，并用结点6的右子树中的最小值去替换结点6的位置，过程是怎么样的。根据上文我们已经很清楚最大最小结点是在哪里，对于以结点8为根结点的右子树中，往左下角（左子树）一直找，得到这个子树的最小结点为结点7。结点7为叶子结点，我们拿掉它不会有其他影响，所以我们直接拿去替换到结点6所在的位置。现在我们看看，结点7由于是原树中结点6的右子树中的最小值，所以在现在的树中，结点7比它的整个右子树都要小；因为原树中结点7在结点6的右子树中，结点7当然会比现在的树中它的左子树都要大。二叉搜索树依然成立，删除完成。

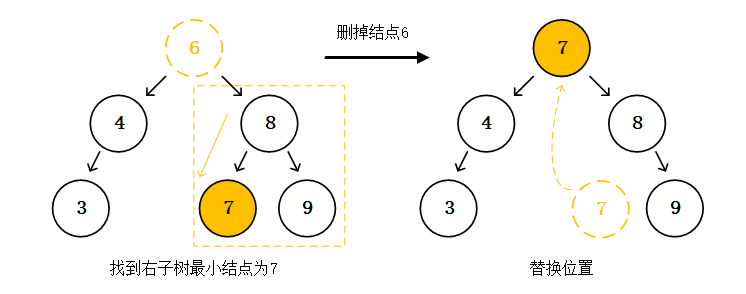
以上删除没有遇到什么问题，因为结点7是叶子结点。现在我们再重新来删除结点6，并用结点6的左子树中的最大值去替换结点6的位置，看看有什么不一样。我们找到结点6的左子树中的最大结点，是结点4，但这次找到后发现结点4并不是叶子结点，它还有一个左子结点，结点4并不在最下层。我们再继续思考，左子树中的最大结点，当它不是叶子结点的时候，它会不会有右子结点呢？显而易见是不会有的，如果有的话应该继续往右子树找，最大结点肯定不是它。所以总结下，在左子树中要么最大的结点是叶子结点，要么最大的结点只有左子结点没有右子结点。放到右子树中也一样，右子树中要么最小结点是叶子结点，要么最小结点只有右子结点没有左子节点。有点绕，但结论是非常简单显而易见的。那回到例子，把不是叶子结点的结点4换去到结点6的位置该怎么做呢？答案很明显，结点4带着它的左子树换到结点6的位置上，并接上结点6的右子树。结点4的左子树依然是结点4的左子树，结点4新的右子树曾经是结点6的右子树，一定比结点4大。二叉搜索树依然成立，删除完成。

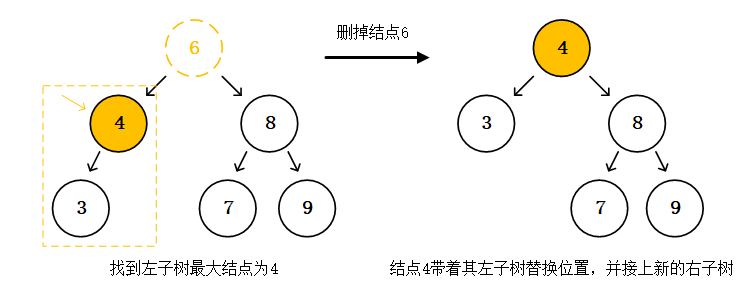
手动实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
public TreeNode remove(int key) {
    TreeNode node = root;
    while(node != null && node.key!=key) {
        if(key<node.key) {
            node = node.left;
        }else if(key>node.key){
            node = node.right;
        }
    }
    if(node==null) {
        return null;
    }

    TreeNode parent = node.parent;
    if(parent!=null && parent.left == node) {
        parent.left = null;
    }else if(parent!=null && parent.right == node){
        parent.right = null;
    }

    if(node.left != null) {
        TreeNode maxOfLeftTree = node.left;
        while(maxOfLeftTree.right!=null) {
            maxOfLeftTree = maxOfLeftTree.right;				
        }
        maxOfLeftTree.parent = parent;
        maxOfLeftTree.right = node.right;
        if(node.right!=null) node.right.parent = maxOfLeftTree;
        if(parent!=null && maxOfLeftTree.key<parent.key) {
            parent.left = maxOfLeftTree;
        }else if(parent!=null && maxOfLeftTree.key>parent.key){
            parent.right = maxOfLeftTree;
        }else {
            root = maxOfLeftTree;
        }

    }else if(node.right != null) {
        TreeNode minOfRightTree = node.right;
        while(minOfRightTree.left!=null) {
            minOfRightTree = minOfRightTree.left;				
        }
        minOfRightTree.parent = parent;
        minOfRightTree.left = node.left;
        if(node.left!=null) node.left.parent = minOfRightTree;
        if(parent!=null && minOfRightTree.key<parent.key) {
            parent.left = minOfRightTree;
        }else if(parent!=null && minOfRightTree.key>parent.key){
            parent.right = minOfRightTree;
        }else {
            root = minOfRightTree;
        }
    }
    node.parent = null;
    node.left = null;
    node.right = null;
    return node;
}