AVL树

严格平衡的二叉搜索树

接上篇二叉树的平衡，我们知道若平衡因子的绝对值越大，这个二叉搜索树就越不平衡，性能就越差，我们面对一些来源未知的数据时，随着不断的插入，一些子树可能会陷入严重不平衡的状态，造成二叉搜索树的效率降低。如果我们规定这样一种二叉搜索树，如果它能达到我们要求的一定平衡条件，那就能保证它的效率不会过于低，这样的二叉搜索树我们叫做平衡二叉树，它有着二叉搜索树的所有性质，你也可以叫它平衡二叉搜索树，平衡二叉树就是满足一些平衡条件的二叉搜索树。当我们设定平衡二叉树的平衡条件为树中的每一个结点的平衡因子的绝对值都不超过1时，我们就得到了AVL树。所以AVL树是平衡条件严格的平衡二叉树，树中每一个结点的平衡因子绝对值都是1或者是0，也就是每一个结点的左右子树高度差最多为1。这篇二叉搜索树中的二叉搜索树例子，它就是一个AVL树。

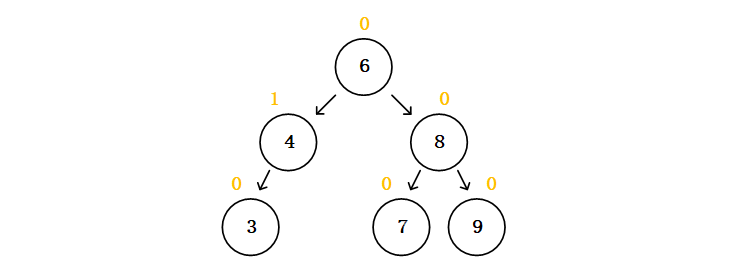
所以在AVL树中，我们必须使用一些办法使得树搜着数据的插入也能保持着平衡条件。这时候我们可以使用一种方法，在每次插入新数据时都去检查这棵树是否平衡，如果不平衡我们将调整一下不平衡的结点，给它们互换下位置，重新让二叉搜索树平衡起来，满足AVL树的条件。

最小不平衡子树

这里先分析一下，我们是每一次做插入操作就去检查一次平衡，若不平衡就调整到平衡，所以我们每次插入前，AVL树都是平衡的，满足AVL树条件的。若现在开始插入操作，插入后导致了不平衡，那从插入节点往父节点一直向上找，找到第一个平衡因子的绝对值大于1的结点，以这个结点为根的子树，我们称为最小不平衡子树。不平衡子树的根结点是一个离插入结点最近的，平衡因子绝对值大于1的结点。这个子树是不平衡的，如果恢复平衡，我们就要从这个子树入手。