二叉树的平衡

上一篇写到二叉搜索树，它平均都是对数的时间复杂度都很优秀。现在考虑一种情况，我们将一组上升序列[1,2,3,……,98,88,100]一共100个值作为结点形成一个新的二叉搜索树，我们插入的第一个结点键为1，最后一个结点的键位100。

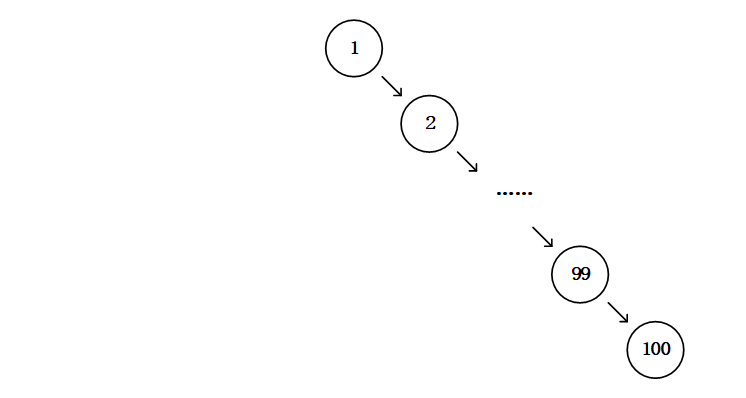
插入完之后我们发现这根本就是一个链表，对于这个二叉搜索树来说，插入查找和删除操作的时间复杂度都不是对数了，因为它是一个普通的链表。我们插入的数据一直都是升序的，对于二叉搜索树的插入方法来看，最终的结果只能是这样的一个链表，完全丧失了二叉搜索树的特性。虽然这个例子很极端，但是说明了一个问题，插入的数据越有序，我们得到的二叉搜索树就越接近链表，时间复杂度就离对数越来越远，查找效率越来越差。

这里就引入了一个问题，怎么样来衡量一个二叉树/二叉搜索树接近链表的程度？更普通来讲，二叉树有左子树和右子树，当二叉树的左右子树高度相差越大时，它就越接近链表，极端情况，当遍历的每一个结点的左右子树，其中一个子树的高度为0时，也就是只存在其中一个子树时，它就完全退化成了链表。所以这个问题变成了怎么样来表示一个二叉树左右子树高度差？显而易见，我们用一个结点的左子树高度减去右子树的高度，得到一个值，这个值越小，右子树比左子树越高，反之这个值越大，左子树比右子树越高，当这个值为0时，这个结点的左右子树达到了平衡。这个值我们称为这个结点的平衡因子，它就能衡量这个树是否平衡。下面我拿上一篇二叉搜索树的二叉树例子看看各个结点的平衡因子。

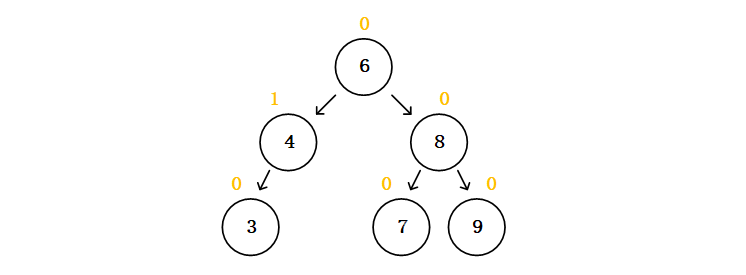
可以看到除了结点4是不平衡的，左子树高度为1，右子树没有所以高度为0，它的平衡因子为1。再说说上面从1插到100的二叉树，根结点1的平衡因子为-100，因为左子树高度为0，右子树高度为100。