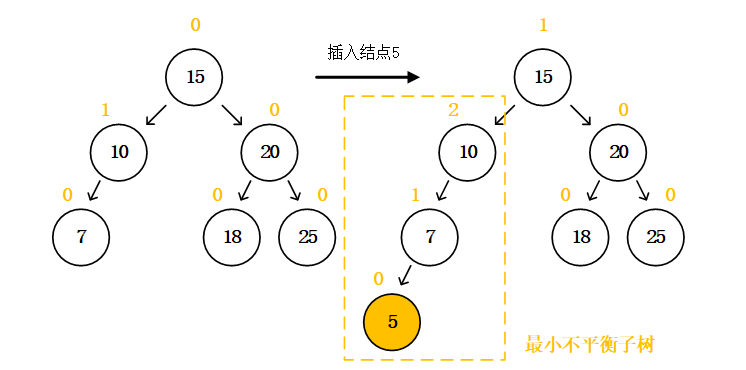
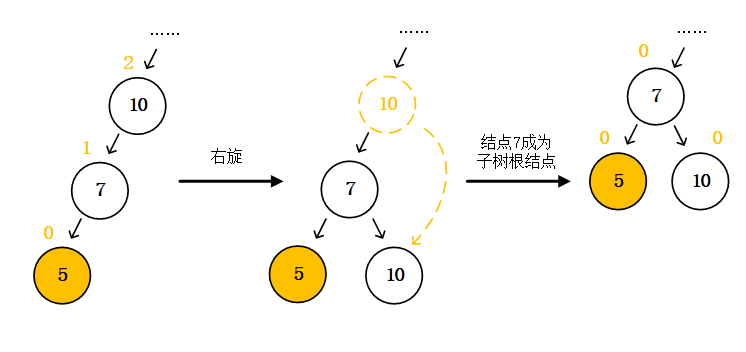
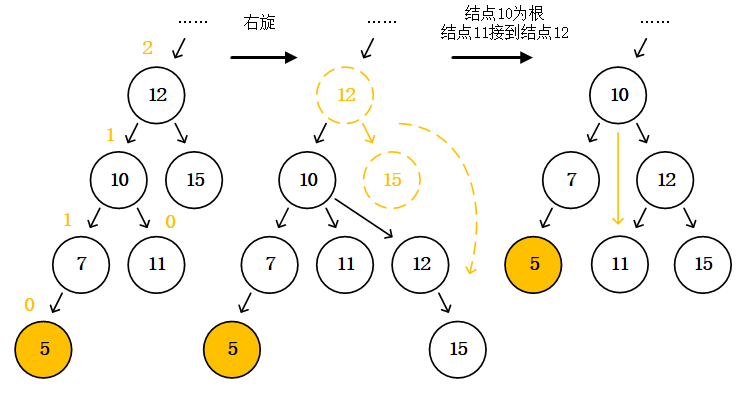
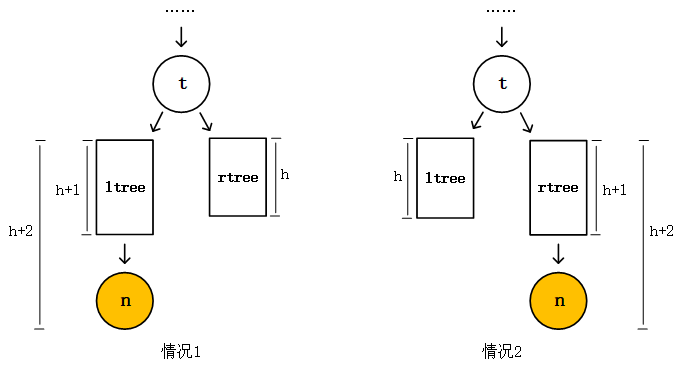
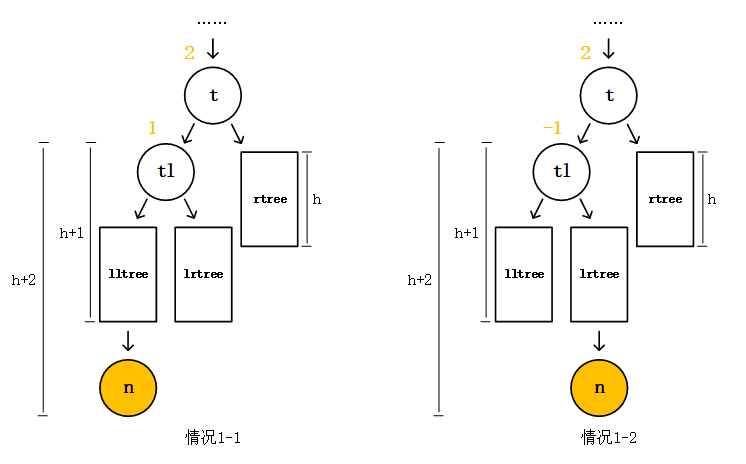
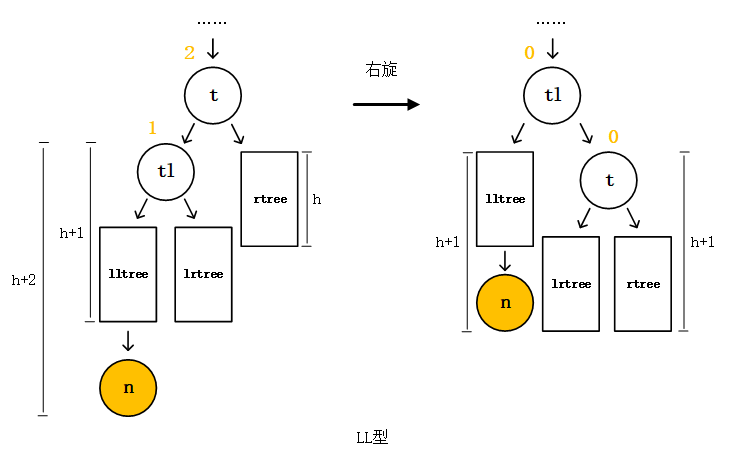
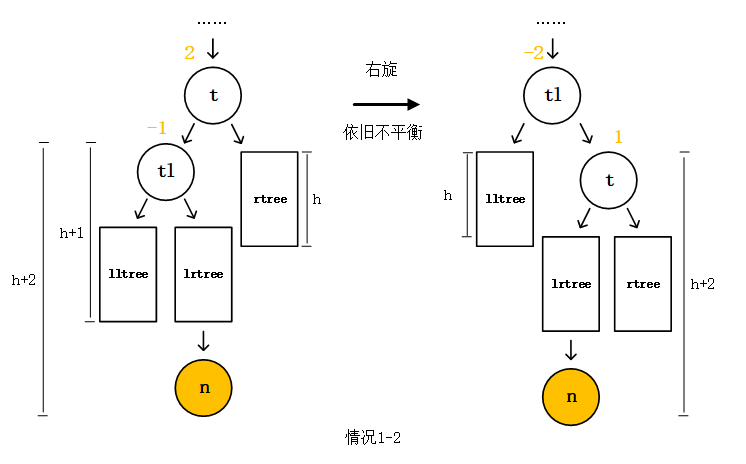
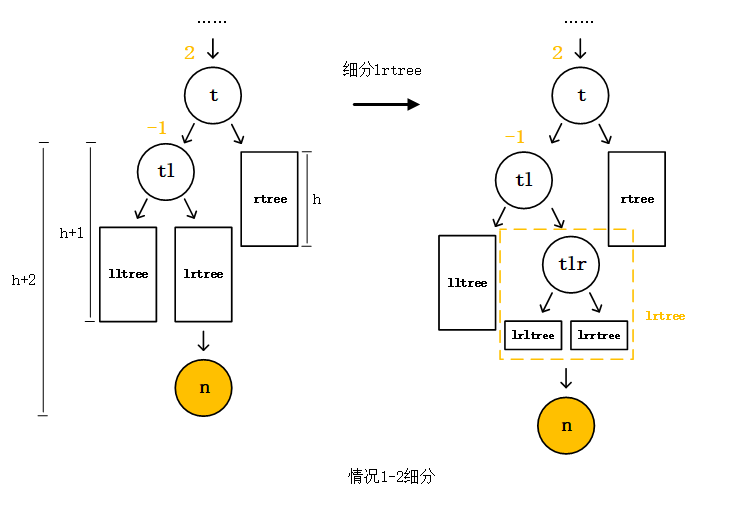
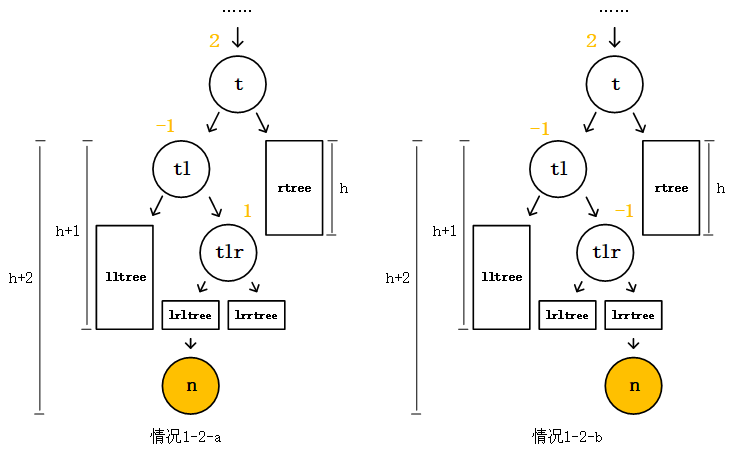
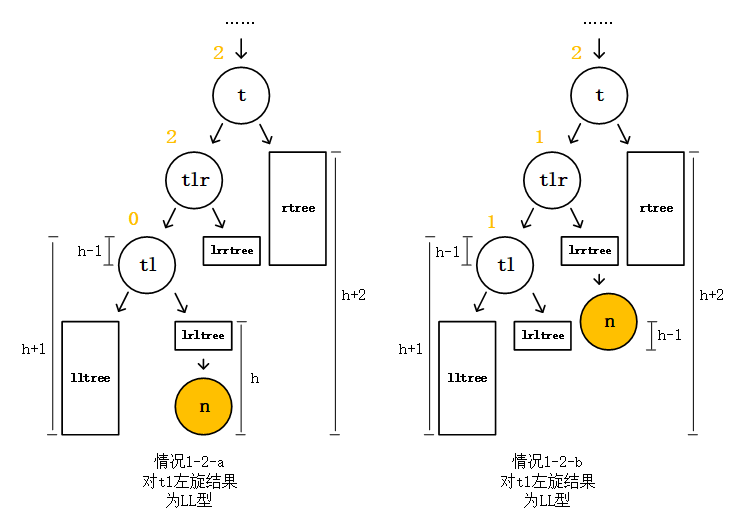
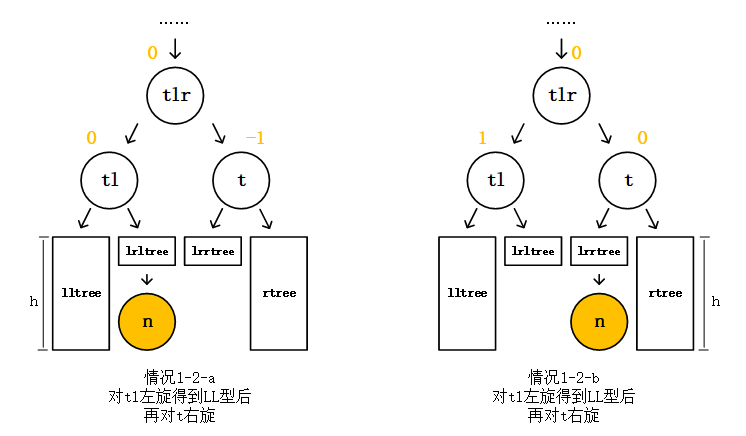
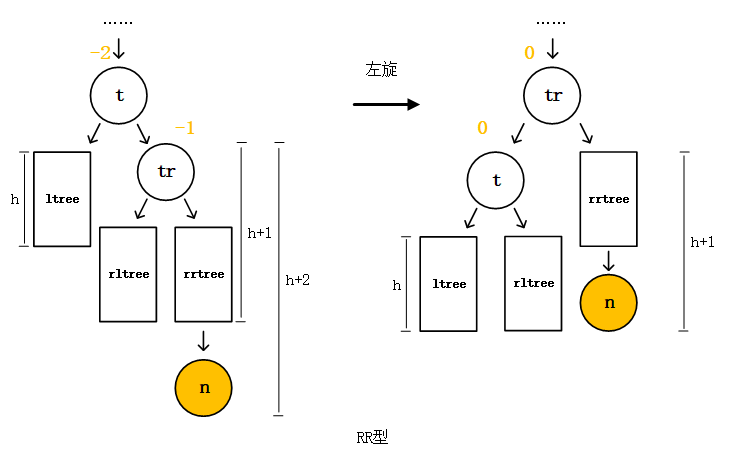
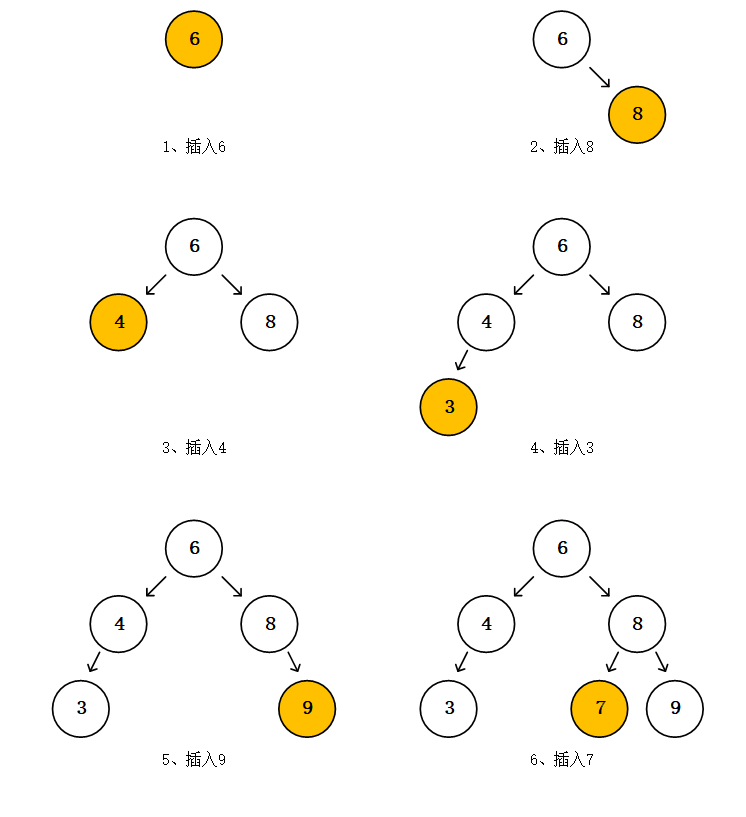
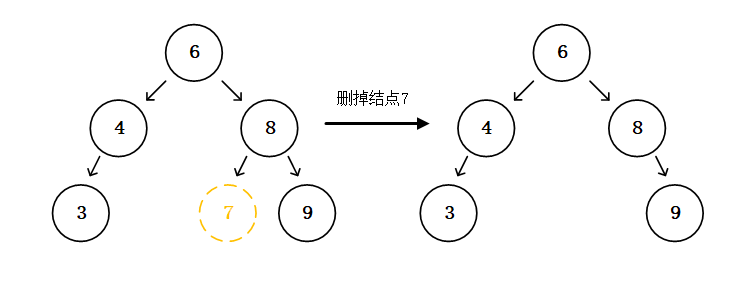
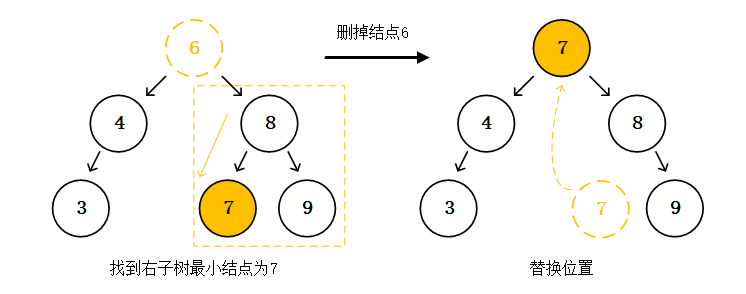
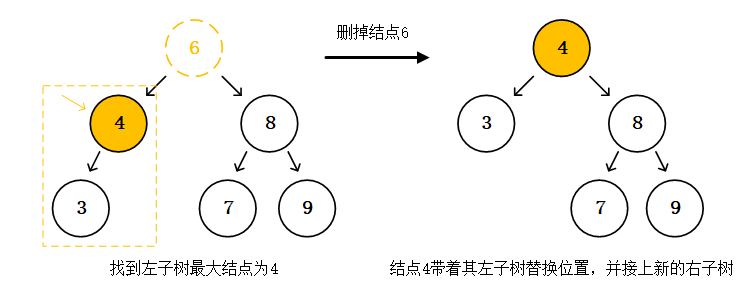
Buffer和TypedArray
不想写await/sync,又不想嵌套括号,于是偷懒用了sync-request,两行就完成了GET请求,但是返回的结果对象,内部有三个字段,headers是对象,url是字符串,唯独body是一串二进制不能直接阅读,需要处理的数据。主要很奇怪的是在编辑器上console出来,控制台显示这是一个uint8Array,调试显示的也是一个uint8Array,但在终端补全时候提示却是一个Buffer。instanceof这两个都是true,unit8Array和Buffer是一个东西吗?
1 | const request = require('sync-request'); |
Buffer和Uint8Array的继承关系:
1 | const buffer = new Buffer(3); |
buffer继承于Uint8Array
Buffer Uint8Array与ArrayBuffer的关系
ArrayBuffer是一段字节,一段二进制数据,可以看做是内存上的一片格子,实质上是内存上一片连续空间的引用,它就代表了这一片连续的空间。ArrayBuffer不能更改长度容量,也不能直接操作它读取上面的数据。
为了操作它,读写上面的数据,我们需要Buffer Uint8Array这些东西,我们称它们为视图(view) ,可以想象Uint8Array覆盖在ArrayBuffer这一片连续内存之上,我们透过这一层视图来操作内存上的数据。
除了Uint8Array以外,ArrayBuffer的视图还有Uint16Array,Uint32Array诸如此类,看命名就可以得知,它们的区别只有bit大小不同,Uint8Array是8bit,1个byte,后两者分别是2个byte和4个byte,这个byte的区别是它们分别用多大的“尺寸”去“解释”ArrayBuffer,它们视图就像翻译机,我们偷着覆盖在上面这层翻译机翻译出下面的数据,Uint8Array是以每1个byte为单位作为一个元素,而Uint16Array是以每2个byte为单位作为一个元素,Uint32Array则是4个byte作为一个单位。他们统称为TypedArray。
如1111 1111 1111 1111 1111 1111 1111 1111这段数据,
Uint8Array解释为[255,255,255,255](十进制)
Uint16Array解释为[65535,65535](十进制)
Uint32Array解释为[33554431](十进制)
而Buffer继承自Uint8Array,自然也是1个字节为一个单位
这类视图有一个统称TypedArray,它们的方法都相同也比较简单,类似于数组的处理。
ArrayBuffer的实例化
1 | new ArrayBuffer(length); |
ArrayBuffer的构造函数只接受一个length参数,实例化出一个有着byte长度为length的内存块的ArrayBuffer实例,当实例化后,这片内存全为0。
注意,没有用数组或者其它buffer作为参数的构造方法,ArrayBuffer本身意义上就是一块连续内存上二进制数据的引用,而现成的数组或者其它buffer内部本身也指向了一块二进制数据。
TypedArray的实例化
1 | new TypedArray(buffer [, byteOffset [, length]]); |
如果说TypedArray这种视图只是一层在ArrayBuffer之上的操作工具,那严格来说它本身是没有数据的,先从ArrayBuffer的实例开始, buffer可以是一个ArrayBuffer的实例,这样实例化出来的TypedArray实例将指向这个ArrayBuffer实例
1 | const arrayBuffer = new ArrayBuffer(4); |
buffer是TypedArray的一个属性,它是视图对象所对应的内存区域,也就是此实例所指向的ArrayBuffer实例。
再来看看可选参数,byteoffset代表的是TypedArray实例指向ArrayBuffer实例的偏移量,单位是byte,默认为0,length代表的是TypedArray实例覆盖ArrayBuffer实例的长度,这个默认不是ArrayBuffer实例的长度,默认是ArrayBuffer实例的长度减去byteoffset,如果byteoffset为ArrayBuffer实例的长度,那length就为0。
1 | const arrayBuffer = new ArrayBuffer(4); |
可见,实例view操作的是arrayBuffer的第一第二个字节。view[3]如果打印出来是undefined。
arrayBuffer为ArrayBuffer对象的实例,它是内存上真实存在的一段空间的引用,一串二进制数据看,这样uint8Array就成为了这一段内存空间引用的视图、操作工具。
现在来试一试,如果接受的参数不是ArrayBuffer实例,而是一个可迭代的数组对象,那实例化出来的TypedArray所指的ArrayBuffer实例是什么,跟传入的数组这个参数有什么关系
1 | const array = [0,0,0,0]; |
很明显,它复制了一份数据,新建了一个ArrayBuffer实例,而view对象指向的就是这个新建的ArrayBuffer实例,视图对象跟数组已经没有关系了。也就是说除了直接给ArrayBuffer实例作为参数是直接指向,不然都是复制一份新的数据(因为数组内部没有指向的ArrayBuffer)。
包括参数为其他TypedArray也是如此,也是复制,而且这个构造函数没有可选偏移量跟长度。
1 | new TypedArray(typedArray); |
多个视图可以同时指向的ArrayBuffer相同。
1 | const arrayBuffer = new ArrayBuffer(4); |
那问题来了,我有一个旧的视图,我现在希望实例化一个新的视图,我希望这两个视图都指向同一片内存数据,又改怎么做呢?直接用旧视图作为构造参数去实例化当然是不行的,那样只会在内存上复制一份新的数据。由于直接使用ArrayBuffer的对象,即用这一块内存数据的引用去实例化视图,才使得视图直接指向这块内存,不会复制新的数据,那我们取出旧视图的代表了内存引用的ArrayBuffer对象,用它去实例化新视图不就可以了吗?
1 | const view1 = new Uint8Array([0,0,0]); |
除了传入ArrayBuffer实例和TypedArray实例,还可以传入一个number值作为构造参数。
1 | new TypedArray(length); |
也可以使用默认构造方法,内部同样会创建一个ArrayBuffer实例并指向它,但其长度为0。
1 | const view = new Uint8Array(); |
from
TypedArray.from()可以获得一个新实例
1 | TypedArray.from(source[, mapFn[, thisArg]]) |
但问题是这个source只能是其他的TypedArray或者可迭代的对象比如数组,也就是不能是ArrayBuffer实例。如果硬要传递进去,只会创建一个新的长度为0ArrayBuffer实例
1 | const arrayBuffer = new ArrayBuffer(4); |
当参数是数组或者其他TypedArray时,是跟构造方法是一样的,复制一份内容。
1 | const array = [0,0,0,0] |
由此可见from方法只能复制,不能共用一段内存数据
可选参数mapFn是个函数,可以类比于数组的map,可以处理每一个元素;thisArg是mapFn的this参数
Buffer
from
那Node的Buffer继承自Uint8Array,大部分跟Unit8Array一致,其中有一些不同的点,比如构造函数Buffer()已经废弃了,要获得一个Buffer实例需要用到Buffer的静态方法from。
from可以传入数组和Buffer实例,没有可选参数,跟TypedArray的构造方法new TypedArray(array)和new TypedArray(buffer)也是一致的,会复制一份数据。
它接受参数为ArrayBuffer实例时,有两个可选参数,byteoffset和length。这里的参数跟TypedArray的构造方法new TypedArray(buffer [, byteOffset [, length]])也是一致的,实例化的行为上也一样,都是直接使用传入ArrayBuffer实例,不会再复制一份数据。
1 | Buffer.from(array) |
1 | const array = [0,0,0,0]; |
1 | const array = [0,0,0,0]; |
1 | const arrayBuffer = new ArrayBuffer(4); |
Buffer内存池
Buffer用Buffer.from()这个静态方法来获取实例化,跟TypedArray直接用构造方法相比,看起来确实一样,但其实会遇到一点问题:
1 | const array = [0,0,0,0]; |
1 | const array = [0,0,0,0]; |
buffer1与buffer2竟然是同一个ArrayBuffer实例。可是buffer1修改了数据在buffer2却是没有变化的。
证明了buffer1与buffer2指向的是同一个ArrayBuffer实例,却是不同的位置,也就是说它们是有偏移量的。
1 | //接着上面的代码 |
view2的起始位置是从ArrayBuffer实例的第616位开始的。
这里插一下队看看Buffer的另两个方法
1 | Buffer.alloc(size[, fill[, encoding]]) |
这两个静态方法实例化出size大小的Buffer实例,它们的一个重要区别是allocUnsafe会在利用Buffer模块的内存池。模块预先分配了一个内存池,大小可以通过属性Buffer.poolsize得到。整个池有一个ArrayBuffer引用,当调用allocUnsafe调用时,检查size大小,如果size小于Buffer.poolsize的一半,直接将现成的内存池,也就是现成的ArrayBuffer引用分配给即将实例化的Buffer,否则,会新开一个内存池,当然,内存池不够大了也会开一个新的,并且下一次allocUnsafe的时候检查的就是这个新的池了。
除了allocUnsafe(size),还有from(array)``from(string)``from(buffer)都是会用到这个机制,所以上面buffer11和buffer2经过检查后size都小于池子大小的一半,分配到的内存的引用都是同一个,只不过他们指向的都不是同一片区域,因为他们的偏移量不同,但是它们确实是在同一个ArrayBuffer里面。
所以利用这个机制我们也很容易可以将两个Buffer实例完全操作一样的内存区域。只要偏移量也相同长度也相同即可。
1 | const array = [0,0,0,0]; |
总结
ArrayBuffer是内存上一片连续数据的引用,它不能操作数据。Buffer和TypedArray有继承关系,TypedArray是ArrayBuffer的视图,用于操作二进制数据实例化
TypedArray靠它的构造函数,参数为可迭代的对象、其他TypedArray实例时,会复制一份新的数据,当参数为ArrayBuffer实例时,直接指向这个实例,同时还可以通过两个可选参数控制对于ArrayBuffer实例的长度和偏移。获取实例还可以使用静态方法from,只能传可迭代的对象作为参数,但两个可选参数,用来处理每一个元素。实例化
Buffer的构造函数已经废弃,实例可以靠静态方法from获得,与上面一样,当参数是可迭代的对象或者其他Buffer实例时,会复制一份数据,当参数是ArrayBuffer的实例时,直接指向它,同时可以控制长度和偏移。Buffer有内存池机制,当实例化Buffer时如果参数不是ArrayBuffer时,会检查Buffer实例的大小,如果小于内存池的一半则将现有的内存池分配给它,否则新建一个内存池。